
Thomas Malthus wrote that all life forms, including humans, have a propensity to exponential population growth when resources are abundant but that actual growth is limited by available resources. So the population growth will stop when overall resources get limited. If the population is already huge having another kid might not be so conducive. Making it somewhere in between arithmetic and geometric progressions. In reality, these are ideal cases, most of the natural phenomenon will have both global and local influencers. In general singular decisions can be anything - but typically arithmetic. There are exceptions of course like the ball bouncing is geometric even though it is singular because of coefficient of restitution. The child who swings extra each time is likely to give only a constant extra force each time, so it is not likely for that to be geometric, it will be an arithmetic progression. If you add a fixed amount to your piggy bank each week that is arithmetic progression. On the other end global/singular decisions give arithmetic progressions. Email chains, Interest rate, etc are more examples of the same kind. In other words that is why there is "half-life" of a radioactive element, in a fixed amount of time it becomes half. Each radioactive atom independently disintegrates, which means it will have fixed decay rate. So population growth each year is geometric. For example population growth each couple do not decide to have another kid based on current population.

Geometric progressions happen whenever each agent of a system acts independently. Using the examples other people have given. As its concepts play a huge role in the arithmetic part of mathematics.I like to explain why arithmetic and geometric progressions are so ubiquitous.
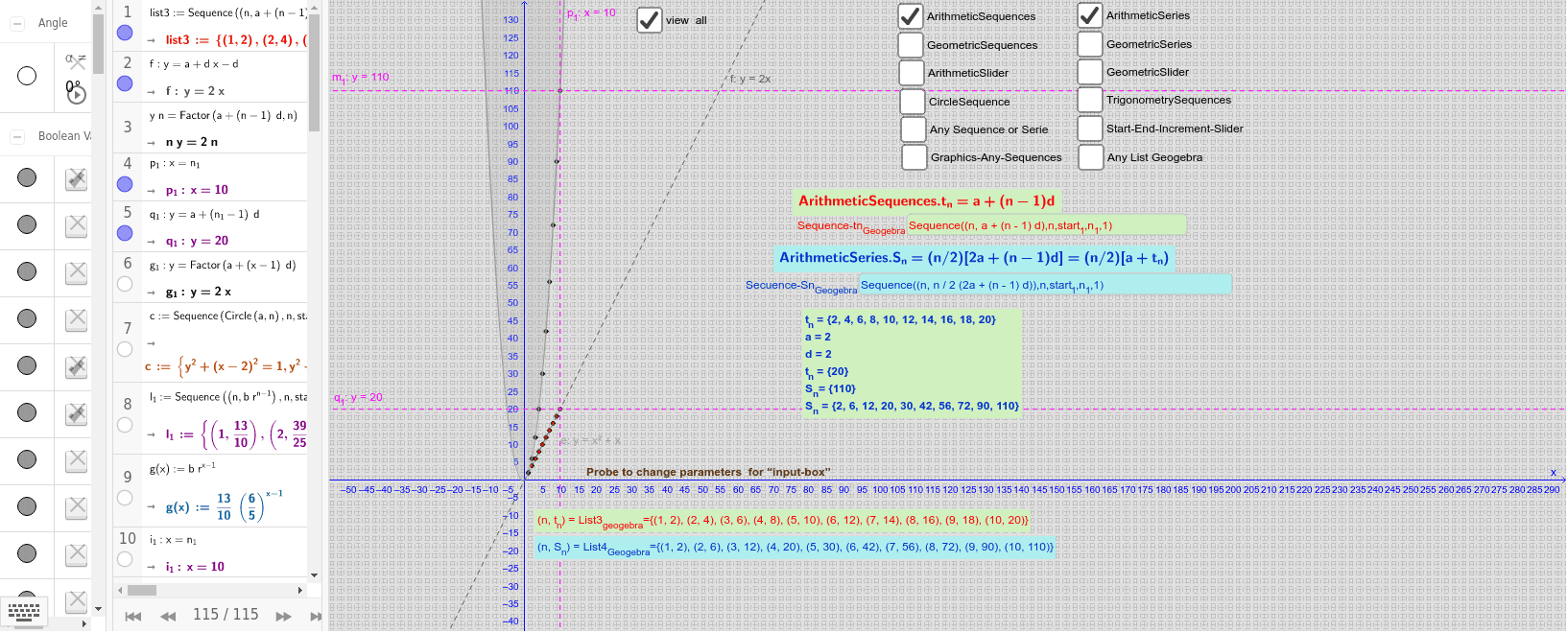
ARITHMETIC AND GEOMETRIC SEQUENCES AND SERIES SERIES
It is recommended that you must understand sequence and series thoroughly. The general form of an arithmetic progression is given by,Īlso,If In an Arithmetic Progression, if “a” is the first term and “d” is the common difference, Then It is to be noted, that this difference can be positive, negative, or zero.Įach number in the Arithmetic Progression is called a term. The fixed difference between the consecutive terms is called the “ common difference” of the Arithmetic Progression.It is denoted by “d”.

In other words, It is a sequence in which each term increases or decreases by a fixed constant. In the Sequence and Series topic we will learn the followingĪrithmetic Progression(A.P.) – In an arithmetic progression, the difference between the two consecutive terms is always the same. If we add all the number of the above sequence, To elaborate, let us take an example from above. SERIES– The sum of the elements of the sequence is called a series. Here the pattern is – “Each element is +1 greater than the previous element”. SEQUENCE– A sequence can be defined as a proper arrangement of elements in a particular order.Each elements in the sequence are separated by “comma(,)”.ġ, 2, 3, 4, … are in sequence. Let us understand the sequence and series mathematically. Thus, the days in week occur in sequence.In school morning assembly teachers tells the students to stand according to your height. Like the days of the week Monday comes after Sunday, Tuesday comes after Monday and so on. If you notice most of the things around us happens in sequence and series. We often come across the word “ sequence and series” in our everyday life. Math Formulas for SSC Exams Menu Toggle.Trigonometric ratios of 90+theta,90-theta,180+theta etc.

Trigonometric Table from 0 to 360 degree.


 0 kommentar(er)
0 kommentar(er)
